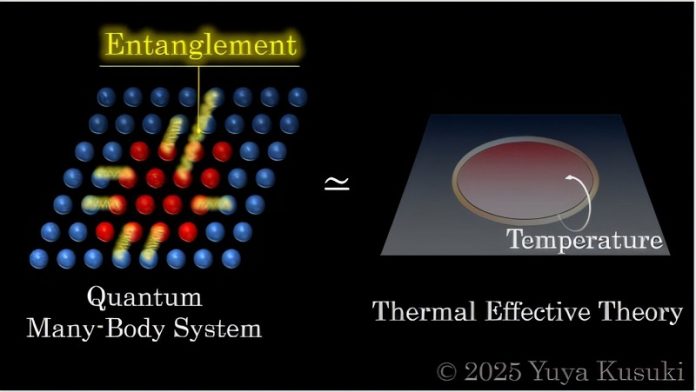
In a breakthrough that could reshape our understanding of quantum physics, a team of researchers has discovered that quantum entanglement follows universal rules, no matter how many dimensions are involved.
Their findings, published in Physical Review Letters, reveal that a tool from particle physics—called thermal effective theory—can be used to understand the structure of quantum entanglement in ways never achieved before.
Quantum entanglement is one of the strangest and most important features of quantum physics.
Unlike in classical physics, where two far-apart particles behave independently, quantum physics allows particles to be deeply connected, or “entangled,” regardless of distance.
This property is the foundation for emerging technologies such as quantum computers and quantum communication systems. Understanding the structure of this entanglement is a major challenge, but it is essential for both practical applications and fundamental theory.
One key way to measure quantum entanglement is with something called Rényi entropy. This mathematical quantity tells scientists about the complexity of quantum states and how information is distributed within them.
Rényi entropy is not only important for classifying quantum states but also plays a role in problems at the cutting edge of physics, such as the mystery of whether information is lost in black holes and studies of quantum gravity.
So far, most research on the structure of quantum entanglement has focused on relatively simple systems—those with just one spatial dimension plus time, known as (1+1)-dimensional systems.
In higher dimensions, the mathematics becomes far more complicated, and progress has been slow.
But the team led by Associate Professor Yuya Kusuki of Kyushu University, working with Professor Hirosi Ooguri and researcher Sridip Pal of the California Institute of Technology and the University of Tokyo’s Kavli Institute for the Physics and Mathematics of the Universe, found a way forward.
They turned to thermal effective theory, a framework originally developed for particle physics to find universal behavior in complex systems.
The theory works on the idea that many physical properties can be described using just a few key parameters, even in very complicated situations. Applying this to quantum information theory, the researchers studied how Rényi entropy behaves in higher-dimensional systems.
They found that when the “replica number” (a parameter in Rényi entropy calculations) is small, the entropy’s behavior is determined by just a few parameters—one of which is the Casimir energy, a fundamental quantity in physics. This universality holds true in any number of dimensions, not just in (1+1)-dimensional systems.
Using these insights, the team also examined the “entanglement spectrum,” which describes the range of possible quantum correlations in a system, and uncovered how its universal properties shift depending on how the Rényi entropy is calculated.
This work marks the first time that thermal effective theory has been applied to quantum entanglement in higher dimensions.
The researchers now plan to refine and expand the approach, aiming to open up new ways to analyze complex quantum systems. Beyond deepening our theoretical understanding, this method could improve simulations of higher-dimensional quantum systems, suggest new ways to classify quantum states, and even provide fresh perspectives on quantum gravity.
In short, this discovery shows that the strange and intricate patterns of quantum entanglement are governed by the same underlying rules everywhere—whether in our familiar three-dimensional world or in realms of many more dimensions.



